AI makes mathematical breakthrough with novel solution

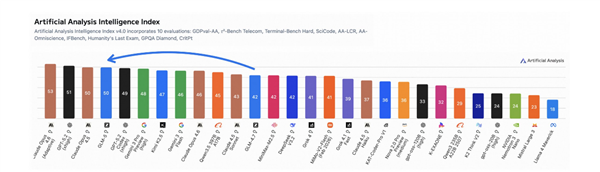
In a significant development for both artificial intelligence and pure mathematics, OpenAI's GPT-5.2Pro model has successfully tackled problem #281 in number theory - the famous Erdős problem. What makes this achievement remarkable isn't just that an AI solved it, but how it did so.

Fields Medalist Terence Tao, one of the world's most respected mathematicians, described the solution as "one of the most explicit cases" of AI cracking open mathematical problems. The proof stood out because it followed a completely different path from previous attempts, suggesting the model wasn't simply replicating existing approaches.

The human behind the machine

The breakthrough came through collaboration between AI and human researcher Neel Somani. While earlier proofs may have provided some background reference points, Tao confirmed the model's approach was genuinely novel. This wasn't GPT-5.2Pro's first attempt at the problem either - records show it had produced an autonomous solution weeks earlier on January 4, 2026.

A reality check on AI's capabilities

As excitement builds about this achievement, mathematicians urge caution about overestimating what AI can do. Tao points out that we mostly see AI's successes while its many failures go unpublished. A tracking database maintained by Paata Ivanisvili and Mehmet Mars Seven reveals the sobering truth: AI succeeds in solving such problems only 1-2% of the time, with most victories coming on easier questions.

"These tools are incredibly valuable," explains one researcher who asked not to be named, "but they're more like powerful calculators than independent thinkers. What's exciting here is how it found a path we hadn't considered."

What this means for mathematics

The mathematical community sees this development as opening new possibilities rather than threatening human researchers:

• Original thinking: GPT-5.2Pro's proof followed logic different from traditional approaches
• Limited but valuable: While success rates remain low overall, these tools can suggest fresh perspectives
• Collaborative future: The best results come from humans and AI working together rather than competing

The Erdős problem solution demonstrates how AI can serve as what mathematicians call "an intuition pump" - sparking new ways of thinking about stubborn problems. As these tools improve, they're likely to become standard equipment in mathematical research, much like computers did decades ago.

Key Points:

• Breakthrough Solution: GPT-5.2Pro developed an original proof for the Erdős problem that impressed experts
• Real Success Rates: Tracking shows AI solves such problems just 1-2% of time, mostly easier ones
• Research Evolution: Mathematicians see AI as valuable new tool rather than replacement