The Arithmetic Struggles of Large Language Models
The Arithmetic Struggles of Large Language Models
Large language models (LLMs) have made significant strides in performing a variety of tasks, including writing poetry, coding, and engaging in conversations. However, despite their impressive capabilities, these AI systems often struggle with basic arithmetic, leading to the conclusion that they are essentially 'math novices.' A recent study has unearthed the underlying reasons for this phenomenon, revealing that their arithmetic reasoning depends heavily on a strategy referred to as 'heuristic hodgepodge.'
The Heuristic Hodgepodge Strategy
According to the research, LLMs do not utilize sophisticated algorithms or rely solely on stored information; instead, they adopt a method akin to a student who has not thoroughly studied mathematical principles. This approach involves making educated guesses based on a mix of learned rules and patterns rather than following a systematic method.
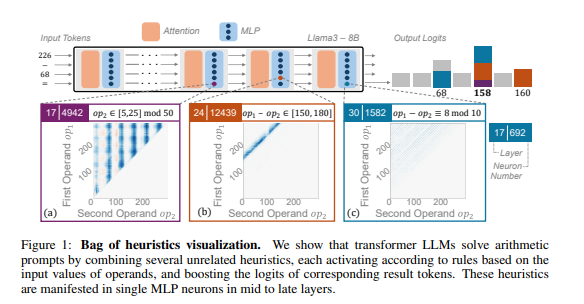
Researchers conducted an in-depth analysis of several prominent LLMs, including Llama3, Pythia, and GPT-J, focusing specifically on their arithmetic reasoning abilities. They discovered that the neural circuitry responsible for arithmetic calculations is composed of numerous individual neurons. Each neuron acts as a 'mini-calculator,' tasked with identifying specific numerical patterns and generating corresponding outputs. For instance, one neuron may focus on recognizing numbers that end in 8, while another could be dedicated to operations that yield results between 150 and 180.
Random Combination of Tools
These 'mini-calculators' operate in a disorganized manner, as LLMs do not employ them through a defined algorithm. Instead, they randomly combine these neural tools based on the input they receive, leading to varied results. This process is comparable to a chef who improvises a dish without a fixed recipe, relying on whatever ingredients are at hand.
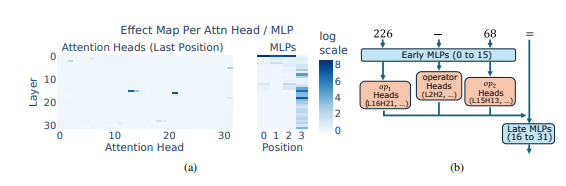
Interestingly, the study found that this heuristic hodgepodge strategy is not a recent development in LLM training. Rather, it emerged early in their training and was refined as the models continued to learn. This indicates that LLMs have depended on this somewhat chaotic reasoning method from the onset of their training rather than developing it later.
Limitations and Implications
The implications of this quirky arithmetic reasoning approach are significant. Researchers identified that the generalization capability of the heuristic hodgepodge strategy is limited and prone to errors. The finite nature of the model's cleverness means that it may falter when facing novel numerical patterns, similar to how a chef skilled only in preparing 'tomato scrambled eggs' would struggle to make 'fish-flavored shredded pork.'
This research sheds light on the limitations inherent in LLMs' arithmetic reasoning and suggests avenues for future advancements in their mathematical skills. The authors assert that simply relying on existing training techniques and model architectures may not suffice to enhance LLMs' arithmetic capabilities. Instead, innovative strategies must be explored to facilitate the development of stronger and more generalized algorithms, ultimately positioning LLMs to become proficient in mathematics.
For further details, the full research paper can be accessed here.
Key Points
- Large language models struggle with basic arithmetic, often relying on a 'heuristic hodgepodge' strategy.
- This approach combines various learned patterns rather than utilizing systematic reasoning.
- The limitations of this strategy highlight the need for new training methods to improve LLMs' mathematical capabilities.